Thursday, 11 May 2017
Testing The Logistic Model Of Constant Constraint Effects: A Miniature Study
Sociolinguistics, like other fields, decided during the 1970s that logistic regression was the best way to analyze the effects of contextual factors on binary variables. Labov (1969) initially conceived of the probability of variable rule application as additive: p = p0 + pi + pj + … . Cedergren & Sankoff (1974) introduced the multiplicative model: p = p0 × pi × pj × … . But it was a slightly more complex equation that eventually prevailed: log(p/(1-p)) = log(p0/(1-p0)) + log(pi/(1-pi)) + log(pj/(1-pj)) + … .
Sankoff & Labov (1979: 195-6) note that this "logistic-linear" model "replaced the others in general use after 1974", although it was not publicly described until Rousseau & Sankoff (1978). It has specific advantages for sociolinguistics (treating favoring and disfavoring effects equally), but it is identical to the general form of logistic regression covered in e.g. Cox (1970). The VARBRUL and GoldVarb programs (Sankoff et al. 2012) apply Iterative Proportional Fitting to log-linear models (disallowing "knockouts" and continuous predictors). Such models are equivalent to logistic models, with identical outputs (pace Roy 2013).
The logistic transformation, devised by Verhulst in 1838, was first used to model population growth over time (Cramer 2002). If a population is limited by a maximum value (which we label 1.0), and the rate of increase is proportional to both the current level p and the remaining room for expansion 1-p, then the population, over time, will follow an S-shaped logistic curve, with a location parameter a and a slope parameter b:
p = exp(a+bt)/(1+exp(a+bt)). We see several logistic curves below.
Its origin in population growth curves makes logistic regression a natural choice for analyzing discrete linguistic change, and it is extensively used in historical syntax (Kroch 1989) and increasingly in phonology (Fruehwald et al. 2009). However, if the independent variable is anything other than time, it is fair to ask whether its effect actually has the signature S-shape.
For social factors, which rarely resemble continuous variables, this is difficult to do. Labov's charts - juxtaposed in Silverstein (2003) - show that in mid-1960's New York, the effect of social class on the (r) variable and the (th) variable were quite different. For (r), the social classes toward the edges of the hierarchy are more dispersed; the lower classes (0 vs. 1) are further apart than the working classes (2-3 vs. 4-5). This is the opposite of a logistic curve, which always changes fastest in the middle. However, (th) shows a different pattern, which is more consistent with a S-curve: the lower and working classes are similar, with a large gap between them and the middle class groups. Finally, while it is hard to judge, neither variable appears to respond to contextual style in a clearly sigmoid manner.
Linguistic factors offer a better approach to the question. Rather than observe the shape of the response to a multi-level predictor - the levels of linguistic factors are often unordered - we can compare the size of binary linguistic constraints among speakers who vary in their overall rates of use. The idea that speakers in a community (and sometimes across community lines) use variables at different rates while sharing constraints began as a surprising observation (Labov 1966, G. Sankoff 1973, Guy 1980) but has become an assumption of the VARBRUL/GoldVarb paradigm (Guy 1991, Lim & Guy 2005, Meyerhoff & Walker 2007, Tagliamonte 2011; but see also Kay 1978, Kay & McDaniel 1979, Sankoff & Labov 1979).
Recently, speaker variation has motivated the introduction of mixed-effects models with random speaker intercepts. But if the variable in question is binary (and the regression is therefore logistic), a constant effect (in logistic terms) should have larger consequences (in percentage terms) in the middle of the range. If speaker A, in a certain context, shifts from 40% to 60% use, then speaker B should shift from 80% to 90% - not 100%. These two changes are equal in logistic units (called log-odds): log(.6/(1−.6)) − log(.4/(1−.4)) = log(.9/(1−.9)) − log(.8/(1−.8)) = 0.811.
In a classic paper, Guy (1980) compared the linguistic constraints on t/d-deletion for many individuals, but (despite the late year) presented factor weights from the multiplicative model, making it impossible to evaluate the relationship between rates and constraints from his tables. Therefore, we will use the following t/d data sets to attempt to address the issue:
Daleszynska (p.c.): 1,998 tokens from 30 Bequia speakers.
Labov et al. (2013): 14,992 tokens from 42 Philadelphia speakers.
Pitt et al. (2007): 13,664 tokens from 40 Central Ohio speakers.
Walker (p.c.): 4,022 tokens from 48 Toronto speakers.
The t/d-deletion predictor to be investigated is following consonant (west coast) vs. following vowel (west end). In most varieties of English, a following consonant favors deletion, while a following vowel disfavors it. Because the consonant-vowel difference has an articulatory basis, we might expect it to remain fairly constant across speakers. But if so, will it be constant in percentage terms, or in logistic terms? In fact, if deletion before consonants is a "late" phonetic process (caused by overlapping gestures?), we might observe a third pattern, where the effect would be smaller in proportion to the amount of deletion generated "earlier".1
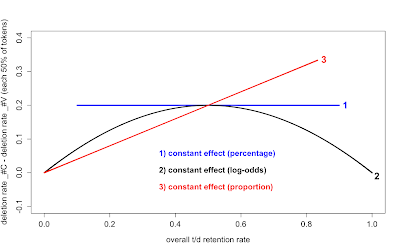
That is, if a linguistic factor - e.g. following consonant vs. vowel in the case of t/d-deletion - has a constant effect in percentage terms, we find a horizontal line (1). If the constraint is constant in log-odds terms, as assumed by logistic regression, we see a curve with a maximum at 50% overall retention (2). If the effect arises from "extra" deletion before consonants, it increases in proportion to the overall retention rate (3).
Comparing the four community studies leads to some interesting results. There is a lot of variation between speakers in each community. We already knew that speakers varied in their overall rates of deletion, but the ranges here are wide. In Philadelphia, the median deletion level is 51%, but the range extends from 22% to 71% (considering people with more than 50 tokens). In the Ohio (Buckeye) corpus, the median rate was lower, 41%, with an even larger range, 18% to 73%. The Torontonians (with less deletion) and the Bequians (with more) also varied widely.
We also observe that speakers within communities differ in the observed following-segment effect. For example, in Philadelphia there were two speakers with very similar overall deletion rates, but one deleted 94% of the time before consonants and only 6% before vowels, while the other had 76% deletion before consonants and 20% before vowels. In Ohio, the consonant-vowel effect was smaller overall, with at least as much between-speaker variation: one speaker produced 79% deletion _#C and 4% _#V, while another produced 51% deletion _#C and 38% _#V. While it would require a statistical demonstration, this amount of divergence is probably more than would be expected by chance. If this is the case, even within speech communities, then we may need to take more care to model speaker constraint differences (for example, with random slopes).
Excludes speakers with <10 tokens, preceding /n/ and following /t, d/.
What about differences between communities? Clearly, the average deletion rates of the four communities differ: Bequia, the Caribbean island, has the most t/d deletion, while Canada's largest city shows the least. The white American communities are intermediate. Such differences are to be expected. What is more interesting is that the largest absolute following-segment effect is found in Philadelphia, where the data is closest to 50% average deletion. Ohio and Toronto, with around 40% deletion, show a smaller effect, in percentage terms. Bequia, with average deletion of nearly 90%, shows no clear following-segment effect at all. These findings are consistent with the logistic interpretation. The effect may be constant - but on the log-odds scale. On the percentage scale, it appears greatest in Philadelphia, where the median speaker shows a difference of 91% _#C vs. 16% _#V. But an effect this large - almost 4 log-odds - should show up in Bequia, yet it does not (of course, the Bequia variety is quite distinct from the others treated here; could it lack this basic constraint?).
Within each community, the logistic model predicts the same thing: the closer a speaker is to 50% deletion overall, the larger the consonant-vowel difference should appear. The data suggest that this prediction is borne out, at least to a first approximation. In Philadelphia, Ohio, and Toronto, all the largest effects are found in the 40% - 60% range, and the smallest effects mostly occur outside that range. While the following-segment constraint differs across communities (larger in Philadelphia, smaller in Bequia), and probably across individual speakers, it seems to follow an inherent arch-shaped curve, similar to (2). A cubic approximation of this curve is superimposed below on the data from all four communities.
In conclusion, the evidence from four studies of t/d-deletion suggests that speaker effects and phonological effects combine additively on a logistic scale, supporting the standard variationist model. However, both rates and constraints can vary, not only between communities, but within them.
Thanks to Agata Daleszynska, Meredith Tamminga, and James Walker.
1A diagonal also results from the "lexical exception" theory (Guy 2007), where t/d-deletion is bled when reduced forms are lexicalized, creating an' alongside and. When a word's underlying form may already be reduced, any contextual effects - like that of following segment - will be smaller in proportion. But if individual-word variation is part of the deletion process, we would expect the logistic curve (2) rather than the diagonal line (3).
References:
Cedergren, Henrietta and David Sankoff. 1974. Variable rules: Performance as a statistical reflection of competence. Language 50(2): 333-355.
Cox, David R. 1970. The analysis of binary data. London: Methuen.
Cramer, Jan S. 2002. The origins of logistic regression. Tinbergen Institute Discussion Paper 119/4. http://papers.tinbergen.nl/02119.pdf.
Fruehwald, Josef, Jonathan Gress-Wright, and Joel Wallenberg. 2009. Phonological rule change: the constant rate effect. Paper presented at North-Eastern Linguistic Society (NELS) 40, MIT. ling.upenn.edu/~joelcw/papers/FGW_CRE_NELS40.pdf.
Guy, Gregory R. 1980. Variation in the group and the individual: the case of final stop deletion. In W. Labov (ed.), Locating language in time and space. New York: Academic Press. 1-36.
Guy, Gregory R. 1991a. Explanation in variable phonology: an exponential model of morphological constraints. Language Variation and Change 3(1): 1-22.
Guy, Gregory R. 1991b. Contextual conditioning in variable lexical phonology. Language Variation and Change 3(2): 223-240.
Guy, Gregory R. 2007. Lexical exceptions in variable phonology. Penn Working Papers in Linguistics 13(2), Papers from NWAV 35. repository.upenn.edu/pwpl/vol13/iss2/9
Kay, Paul. 1978. Variable rules, community grammar and linguistic change. In D. Sankoff (ed.), Linguistic variation: models and methods. New York: Academic Press. 71-83.
Kay, Paul and Chad K. McDaniel. 1979. On the logic of variable rules. Language in Society 8(2): 151-187.
Labov, William. 1966. The social stratification of English in New York City. Washington, D.C.: Center for Applied Linguistics.
Labov, William. 1969. Contraction, deletion, and inherent variability of the English copula. Language 45(4): 715-762.
Labov, William et al. 2013. The Philadelphia Neighborhood Corpus of LING560 Studies. fave.ling.upenn.edu/pnc.html.
Lim, Laureen T. and Gregory R. Guy. 2005. The limits of linguistic community: speech styles and variable constraint effects. Penn Working Papers in Linguistics 13.2, Papers from NWAVE 32. 157-170.
Meyerhoff, Miriam and James A. Walker. 2007. The persistence of variation in individual grammars: copula absence in ‘urban sojourners’ and their stay‐at‐home peers, Bequia (St. Vincent and the Grenadines). Journal of Sociolinguistics 11(3): 346-366.
Pitt, M. A. et al. 2007. Buckeye Corpus of Conversational Speech. Columbus, OH: Department of Psychology, Ohio State University. buckeyecorpus.osu.edu.
Rousseau, Pascale and David Sankoff. Advances in variable rule methodology. In D. Sankoff (ed.), Linguistic Variation: Models and Methods. New York: Academic Press. 57-69.
Roy, Joseph. 2013. Sociolinguistic Statistics: the intersection between statistical models, empirical data and sociolinguistic theory. Proceedings of Methods in Dialectology XIV in London, Ontario.
Sankoff, David, Sali Tagliamonte, and Eric Smith. 2012. Goldvarb LION: A variable rule application for Macintosh. Department of Linguistics, University of Toronto.
Sankoff, David and William Labov. 1979. On the uses of variable rules. Language in Society 8(2): 189-222.
Sankoff, Gillian. 1973. Above and beyond phonology in variable rules. In C.-J. N. Bailey & R. W. Shuy (eds), New ways of analyzing variation in English. Washington, D.C.: Georgetown University Press. 44-61.
Silverstein, Michael. 2003. Indexical order and the dialectics of sociolinguistic life. Language & Communication 23(3-4): 193-229.
Tagliamonte, Sali A. 2011. Variationist sociolinguistics: change, observation, interpretation. Hoboken, N.J.: Wiley.
Subscribe to:
Post Comments (Atom)




No comments:
Post a Comment