I suggested in my last post that in the future, the current system of academic peer review should be replaced by post-publication peer review. A recent publication in PNAS (Proceedings of the National Academy of Sciences) provides a good opportunity for me to attempt such a review myself. Of course, an article published in PNAS has already gone through peer review, but the close relationship between authors and editors there often results in a product that – even more than always – might benefit from some outside criticism.
"Climate, vocal folds, and tonal languages: Connecting the physiological and geographic dots," by Caleb Everett, Damián Blasi and Seán Roberts, is an ambitious, though short paper that argues for a connection between low humidity and temperature and the absence of tone, particularly complex tone (defined as three or more levels of phonemic pitch contrast), in languages around the world.
To make this argument, Everett et al. first cite literature, particularly from laryngology, supporting the idea that pitch distinctions are more difficult to make under dry and cold conditions. And if complex tone is "maladaptive (even in minor ways)," they predict that languages spoken in comparatively arid and/or chilly locales will be more likely to "lose/never acquire" complex tonal contrasts. The majority of the paper is then devoted to demonstrating that the predicted correlation exists: globally, within large language families, and across linguistic isolates.
To me, it was helpful to think of the paper's structure in the opposite direction. Clearly, if the correlation between climate and tone does not exist – or if it does exist, but could be due to chance – then as far as this particular claim is concerned, we could stop right there. However, it would still be worth thinking about the proposed explanation. While ease of articulation and perception are certainly important forces driving language change, the idea that these forces themselves might vary based on totally extra-linguistic factors (like climate) is very intriguing.
But if we do accept Everett et al.'s argument, we might also expect that many other small differences in people's environments should differentially favor changes to their language over the long term. So assuming more phonetic predictions of this type can be made, the theory would have a problem if the geographical correlations don't pan out as well as they seem to in this case. Also, if we extend our interest to small differences in people's anatomy in different parts of the world, we might be treading on ground that is considered, at least since the mid-twentieth century, rather dangerous.
Returning to the specifics of the article, the argument that dry and cold air negatively affects the production of precise pitch differences is well-supported, but the magnitude of these effects is never made clear. While the evolutionary argument does not depend on the effects being large, it would have been nice to know, for example, if the increased imprecision in pitch when "jitter measurements increased by over 50%" were comparable in magnitude to tonal pitch differences, or not. It is also relevant that language hearers typically "normalize" or compensate for phonetic differences of considerable size in the speech of their interlocutors. This point, and more generally the relationship between pitch (a phonetic property) and tone (a phonological one) was not considered.
Surprisingly, in the section about the geographic correlation, no quantitative estimate is ever given of the effects of humidity (or temperature) on the likelihood of a language having complex tone. This information is presented in a cumulative distribution plot (Figure 2), which does have the advantage (from the authors' point of view) of maximizing the appearance of the effect.
When numbers are presented, they compare the climate properties of tonal vs. non-tonal languages, rather than treating climate as the explanatory variable it is claimed to be. This may seem like a quibble, but it makes it rather difficult to understand just how strong an association is being shown. For example, when we read that "the average [humidity] for isolates with complex tone is 0.017, whereas the average for other isolates is 0.013," this measures a difference in average climate (whatever that means), depending on the language type. What the reader deserves to know is how different the tonal properties of languages are, depending on the climate.
Although the bulk of this section quite correctly attempts to eliminate areal effects as an explanation for the association between climate and tone, the final paragraph seemingly does an about-face, suggesting that "tone spreads across languages more effectively via
interlinguistic contact in regions with favorable ambient conditions" and less effectively in cold/dry regions. This expands the scope of the hypothesis beyond language transmission to include language contact, without any additional evidence, and possibly at the risk of circularity.
I would have expected that what linguists already know about tonogenesis would be more relevant to this topic. Mentioning it for the first time in their discussion and conclusions section, Everett et al. say only that this literature does not predict any effect of climate. Actually, this might make perfect sense if languages in dry, cold climates only tend to lose tone, rather than "lose/never acquire" it (to return to the authors' curious conflation). But in this case, some discussion of how tone is ordinarily thought to be lost might have been worthwhile, even if the influence of climate could be independent.
In summary, I found the argument for the geographic correlation itself to be fairly strong, although I did not really look into the details here. The link between the proposed phonetic effect and language change was plausible, but needed more grounding in research on language change in general and the loss of tone in particular. But I was less convinced that the physiological (or phonetic) effects of dry and cold air are really an obstacle to producing phonological tone. Like Everett et al., I too hope "that experimental phoneticians and others examine the effects of ambient air conditions on the production of tones and other sound patterns, so that we can better understand this pivotal way in which human sound systems appear to be ecologically adaptive." Unless they are too busy.
Thursday, 11 May 2017
Are You Talkin' To ME? In defense of mixed-effects models
At NWAV 43 in Chicago, Joseph Roy and Stephen Levey presented a poster calling for "caution" in the use of mixed-effects models in situations where the data is highly unbalanced, especially if some of the random-effects groups (speakers) have only a small number of observations (tokens).
One of their findings involved a model where a certain factor received a very high factor weight, like .999, which pushed the other factor weights in the group well below .500. Although I have been unable to look at their data, and so can't determine what caused this to happen, it reminded me that sum-contrast coefficients or factor weights can only be interpreted relative to the other ones in the same group.
An outlying coefficient C does not affect the difference between A and B. This is much easier to see if the coefficients are expressed in log-odds units. In log-odds, it seems obvious that the difference between A: -1 and B: +1 is the same as the difference between A': -5 and B': -3. The difference in each case is 2 log-odds.
Expressed as factor weights -- A: .269, B: .731; A': .007, B': .047 -- this equivalence is obscured, to say the least. It is impossible to consistently describe the difference between any two factor weights, if there are three or more in the group. To put it mildly, this is one of the disadvantages of using factor weights for reporting the results of logistic regressions.
Since factor weights (and the Varbrul program that produces them) have several other drawbacks, I am more interested in the (software-independent) question that Roy & Levey raise, about fitting mixed-effects models to unbalanced data. Even though handling unbalanced data is one of the main selling points of mixed models (Pinheiro & Bates 2000), Roy and Levey claim that such analyses "with less than 30-50 tokens per speaker, with at least 30-50 speakers, vastly overestimate variance", citing Moineddin et al. (2007).
However, Moineddin et al. actually only claim to find such an overestimate "when group size is small (e.g. 5)". In any case, the focus on group size points to the possibility that the small numbers of tokens for some speakers is the real issue, rather than the data imbalance itself.
Fixed-effects models like Varbrul's vastly underestimate speaker variance by not estimating it at all and assuming it to be zero. Therefore, they inflate the significance of between-speaker (social) factors. P-values associated with these factors are too low, increasing the rate of Type I error beyond the nominal 5% (this behavior is called "anti-conservative"). All things being equal, the more tokens there are per speaker, the worse the performance of a fixed-effects model will be (Johnson 2009).
With only 20 tokens per speaker, the advantage of the mixed-effects model can be small, but there is no sign that mixed models ever err in the opposite direction, by overestimating speaker variance -- at least, not in the balanced, simulated data sets of Johnson (2009). If they did, they would show p-values that are higher than they should be, resulting in Type I error rates below 5% (this behavior is called "conservative").
It is difficult to compare the performance of statistical models on real data samples (as Roy and Levey do for three Canadian English variables), because the true population parameters are never known. Simulations are a much better way to assess the consequences of a claim like this.
I simulated data from 20 "speakers" in two groups -- 10 "male", 10 "female" -- with a population gender effect of zero, and speaker effects normally distributed with a standard deviation of either zero (no individual-speaker effects), 0.1 log-odds (95% of speakers with input probabilities between .451 and .549), or 0.2 log-odds (95% of speakers between .403 and .597).
The average number of tokens per speaker (N_s) ranged from 5 to 100. The number of tokens per speaker was either balanced (all speakers have N_s tokens), imbalanced (N_s * rnorm(20, 1, 0.5), or very imbalanced (N_s * rnorm(20, 1, 1). Each speaker had at least one token and no speaker had more than three times the average number of tokens.
For each of these settings, 1000 datasets were generated and two models were fit to each dataset: a fixed-effects model with a predictor for gender (equivalent to the "cautious" Varbrul model that Roy & Levey implicitly recommend), and a mixed-effects (glmer) model with a predictor for gender and a random intercept for speaker. In each case, the drop1 function (a likelihood-ratio test) was used to calculate the Type I error rate -- the proportion of the 1000 models with p < .05 for gender. Because there is no real gender effect, if everything is working properly, this rate should always be 5%.
For each panel, the figure above plots the proportion of significant p-values (p < .05) obtained from the simulation, in blue for the fixed-effects model and in magenta for the mixed model. A loess smoothing line has been added to each panel. Again, since the true population gender difference is always zero, any result deemed significant is a type I error. The figure shows that:
1) If there is no individual-speaker variation (left column), the fixed-effects model appears to behave properly, with 5% Type I error, and the mixed model is slightly conservative, with 4% Type I error. There is no effect of the average number of tokens per speaker (within each panel), nor is there any effect of data imbalance (between the rows of the figure).
2) If there is individual-speaker variation (center and right columns), the fixed-effects model error rate is always above 5%, and it increases roughly linearly in proportion to the number of tokens per speaker. The greater the individual-speaker variation, the faster the increase in the Type I error rate for the fixed-effects model, and therefore the larger the disadvantage compared with the mixed model.
The mixed model proportions are much closer to 5%. We do see a small increase in Type I error as the number of tokens per speaker increases; the mixed model goes from being slightly conservative (p-values too high, Type I error below 5%) to slightly anti-conservative (p-values too low, Type I error above 5%).
Finally, there is a small increase in Type I error associated with greater data imbalance across groups. However, this effect can be seen for both types of models. There is no evidence that mixed models are more susceptible to error from this source, either with a low or a high number of average tokens per speaker.
In summary, the simulation does not show any sign of markedly overconservative behavior from the mixed models, even when the number of tokens per speaker is low, and the degree of imbalace is high. This is likely to be because the mixed model is not "vastly overestimating" speaker variance in any general way, despite Roy & Levey's warnings to the contrary.
We can look at what is going on with these estimates of speaker variance, starting with a "middle-of-the-road" case where the average number of tokens per speaker is 50, the true individual-speaker standard deviation is 0.1, and there is no imbalance across groups.
For this balanced case, the fixed-effects model gives an overall Type I error rate of 6.4%, while the mixed model gives 4.4%. The mean estimate of individual-speaker variance, in the mixed model, is 0.063. Note that this average is an underestimate, not an overestimate, of the variance in the population, which is 0.1.
Indeed, in 214 of the 1000 runs, the mixed model underestimated the speaker variance as much as it possibly could: it came out as zero. For these runs, the proportion of Type I error was higher: 6.1%, and similar to the fixed-effects model, as we would expect.
In 475 of the runs, a positive speaker variance was estimated that was still below 0.1, and the Type I error rate was 5.3%. And in 311 runs, the variance was indeed overestimated, that is, it was higher than 0.1. The Type I error rate for these runs was only 1.9%.
Mixed models can overestimate speaker variance -- incidentally, this is because of the sample data they are given, not because of some glitch -- and when this happens, the p-value for a between-speaker effect will be too high (conservative), compared to what we would calculate if the true variance in the population were known. However, in just as many cases, the opposite thing happens: the speaker variance is underestimated, resulting p-values that are too low (anti-conservative). On average, though, the mixed-effects model does not behave in an overly conservative way.
If we make the same data quite unbalanced across groups (keeping the average of 50 tokens per speaker and the speaker standard deviation of 0.1), the Type I error rates rise to 8.3% for the fixed-effects model and 5.6% for the mixed model. So data imbalance does inflate Type I error, but mixed models still maintain a consistent advantage. And it is still as common for the mixed model to estimate zero speaker variance (35% of runs) as it is to overestimate the true variance (28% of runs).
I speculated above that small groups -- speakers with few tokens -- might pose more of a problem than unbalanced data itself. Keeping the population speaker variance of 0.1, and the high level of data imbalance, but considering the case with only 10 tokens per speaker on average, we see that the Type I error rates are 4.5% for fixed, 3.0% for mixed.
The figure of 4.5% would probably average out close to 5%; it's within the range of error exhibited by the points on the figure above (top row, middle column). Recall that our simulations go as low as 5 tokens per speaker, and if there were only 1 token per speaker, no one would assail the accuracy of a fixed-effects model because it ignored individual-speaker variation (or, put another way, within-speaker correlation). But sociolinguistic studies with only a handful of observations per speaker or text are not that common, outside of New York department stores, rare discourse variables, and historical syntax.
For the mixed model, the Type I error rate is the lowest we have seen, even though only 28% of runs overestimated the speaker variance. Many of these overestimated it considerably, however, contributing to the overall conservative behavior.
Perhaps this is all that Roy & Levey intended by their admonition to use caution with mixed models. But a better target of caution might be any data set like this one: a binary linguistic variable, collected from 10 "men" and 10 "women", where two people contributed one token each, another contributed 2, another 4, etc., while others contributed 29 or 30 tokens. As much as we love "naturalistic" data, it is not hard to see that such a data set is far from ideal for answering the question of whether men or women use a linguistic variable more often. If we have to start with very unbalanced data sets, including groups with too few observations to reasonably generalize from, it is too much to expect that any one statistical procedure can always save us.
The simulations used here are idealized -- for one thing, they assume normal distributions of speaker effects -- but they are replicable, and can be tweaked and improved in any number of ways. Simulations are not meant to replicate all the complexities of "real data", but rather to allow the manipulation of known properties of the data. When comparing the performance of two models, it really helps to know the actual properties of what is being modeled. Attempting to use real data to compare the performance of models at best confuses sample and population, and at worst casts unwarranted doubt on reliable tools.
References
Johnson, D. E. 2009. Getting off the GoldVarb standard: introducing Rbrul for mixed-effects variable rule analysis. Language and Linguistics Compass 3/1: 359-383.
Moineddin, R., F. I. Matheson and R. H. Glazier. 2007. A simulation study of sample size for multilevel logistic regression models. BMC Medical Research Methodology 7(1): 34.
Pinheiro, J. C. and D. M. Bates. 2000. Mixed-effect models in S and S-PLUS. New York: Springer.
Roy, J. and S. Levey. 2014. Mixed-effects models and unbalanced sociolinguistic data: the need for caution. Poster presented at NWAV 43, Chicago. http://www.nwav43.illinois.edu/program/documents/Roy-LongAbstract.pdf
How Should We Measure What "Doesn't Exist"
I was told the other day that vowel formants don't exist, or that they're not real, or something; that measuring F1 and F2 is like trying to measure the diameter of an irregular, non-spherical object, like this comet:
I can see two ways in which this is true. First, a model of the human vocal tract consisting of two (or even more) formant values is far from accurate: the vocal tract can generate anti-formants, and even without that complication, the shape and material of the mouth and pharynx are not very much like those of a flute or clarinet; the vocal tract is a much more complex resonator. However, most of us are not interested in modeling this physical, biological object as such, nor, unless we are very much oriented towards articulatory phonetics, the movements of the tongue for their own sake. We are more interested in representing the aspects of vowel sounds that are important linguistically.
But here too, the conception that "vowels are things with two formants and a midpoint" is a substantial oversimplification. Most obviously, vowels extend over (more or less) time, and their properties can change (more or less) during this time. Both these aspects - duration and glide direction/extent - can be linguistically distinctive, although they often are not. So to fully convey the properties of a vowel, we will need to create a dynamic representation. While this creates challenges for measurement and especially for analysis, these problems are orthogonal to the question of how best to describe a vowel at a single point - more precisely, a short window - in time.
As mentioned, the "point" spectrum of a vowel sound, a function mapping frequency to amplitude, is complex. For one thing, it contains some information that is relatively speaker-specific. This data is of great importance in forensic and other speaker-recognition tasks, but in sociophonetic/LVC work we are usually happy to ignore it (if we even can). Other aspects of a vowel's spectrum, not necessarily easily separable from the first category, convey information about pitch, nasality, and the umbrella term "voice quality". These things may or may not interest us, depending on the language involved and the particular research being conducted.
And then there is "vowel quality" proper, which linguists generally describe using four pairs of terms: high-low (or closed-open), back-front, rounded-unrounded, and tense-lax. Originally, these parameters were thought of as straightforwardly articulatory, reflecting the position of the jaw, tongue, lips, and pharynx. As we will see, this articulatory view has shifted, but the IPA alphabet still uses the same basic terms (though no longer tense-lax), and for the most part Ladefoged & Johnson (2014) classify English vowels along the same dimensions as A. M. Bell (1867), who used primary-wide instead of tense-lax:
Equally long ago, scientists were beginning to realize that the vocal tract's first two resonances (or formants, as we now say) are related to the high-low and back-front dimensions of vowel quality, respectively. The higher the first formant (F1), the lower the vowel, and the higher the second formant (F2), the fronter the vowel. Helmholtz (1862/1877) partially demonstrated this with experiments holding a series of tuning forks up to the mouth, and he also made the first steps in vowel synthesis. But he found it difficult - like present-day researchers, sometimes - to distinguish F1 and F2 in back vowels, considering them simple resonances:
In contrast to Helmholtz, A. G. Bell (1879) and Hermann (1894) both emphasized that the resonance frequencies characterizing specific vowels were independent of the fundamental frequency (F0) of the voice. Bell provided an early description of formant bandwidth, while Hermann coined the term "formant" itself.
In the new century, experiments on the phonautograph, the phonograph, the Phonodeik, and other machines led most investigators to realize that all vowel sounds consisted of several formants (not just one for back vowels and two for front vowels, as Helmholtz had influentially claimed); advances were also made in vowel synthesis, using electrical devices. In particular, Paget (1930) argued for the importance of two formants for each vowel. But the most progress in acoustic phonetics was made after the invention of the sound spectrograph and its declassification following World War II.
Four significant publications from the immediate postwar years - Essner (1947), Delattre (1948), Joos (1948), and Potter & Peterson (1948) - all use spectrographic data to analyze vowels, and all four explicitly identify the high-low dimension with F1 (or "bar 1" for P & P) and the back-front dimension with F2 (or "bar 2" for P & P). Higher formants are variously recognized, but considered less important. In Delattre's analysis, the French front rounded vowels are seen to have lower F2 (and F3) values than the corresponding unrounded vowels:
Jakobson, Fant and Halle (1952) is somewhat different; it defines the acoustic correlates of distinctive phonological features, aiming to cover vowels and consonants with the same definitions. So the pair compact-diffuse refers to the relative prominence of a central spectral peak, while grave-acute reflects the skewness of the spectrum. In vowels, compact is associated with a more open tongue position and higher F1, and diffuse with a more closed tongue position and lower F1. Grave or back vowels have F2 closer to F1, acute or front vowels have F2 closer to F3. (Indeed, F2 - F1 has been suggested as an alternative to F2 for measuring the back-front dimension, e.g. in the first three editions of Ladefoged's Course on Phonetics).
These authors all more or less privilege an acoustic view of vowel differences over an articulatory view, noting that acoustic measurements may correspond better to the traditional "articulatory" vowel quadrilateral than the actual position of the tongue during articulation. The true relationship between articulation and acoustics was not well understood until Fant (1960). But the discrepancy had been suspected at least since Russell (1928), whose X-ray study showed that the highest point of the tongue was not directly related to vowel quality; it was noticeably higher in [i] than in [u], for example. In addition, certain vowel qualities, like [a], could be produced with several different configurations of the tongue. Observations like these led Russell to make the well-known claim that "phoneticians are thinking in terms of acoustic fact, and using physiological fantasy to express the idea".
Outside of a motor theory of speech perception, the idea that the vowel space is defined by acoustic resonances rather than articulatory configurations should be acceptable, although the integration of continuous acoustic parameters into phonological theory has never been smoothly accomplished. While we don't know that formant frequencies are directly tracked by our perceptual apparatus, it seems that they are far from fictional, at least from the point of view of how they function in language.
[To be continued in Part 2, with less history and more practical suggestions!]
References (the works by Harrington, Jacobi, and Lindsey, though not cited above, were useful in learning about the topic):
Bell, Alexander Graham. 1879. Vowel theories. American Journal of Otology 1: 163-180.
Bell, Alexander Melville. 1867. Visible Speech: The Science of Universal Alphabetics. London: Simkin, Marshall & Co.
Delattre, Pierre. 1948. Un triangle acoustique des voyelles orales du français. The French Review 21(6): 477-484.
Essner, C. 1947. Récherches sur la structure des voyelles orales. Archives Néerlandaises de Phonétique Expérimentale 20: 40-77.
Fant, Gunnar. 1960. Acoustic theory of speech production. The Hague: Mouton.
Harrington, Jonathan. 2010. Acoustic phonetics. In W. Hardcastle et al. (eds.), The Handbook of Phonetic Sciences, 2nd edition. Oxford: Blackwell.
Helmholtz, Hermann von. 1877. Die Lehre von den Tonempfindungen. 4th edition. Braunschweig: Friedrich Vieweg.
Hermann, Ludimar. 1894. Beiträge zur Lehre von der Klangwahrnehmung. Pflügers Archiv 56: 467-499.
Jacobi, I. 2009. On variation and change in diphthongs and long vowels of spoken Dutch. Ph.D. dissertation, University of Amsterdam.
Jakobson, Roman, Fant, C. Gunnar M., and Halle, Morris. 1952. Preliminaries to speech analysis: the distinctive features and their correlates. Cambridge: MIT Press.
Joos, Martin. 1948. Acoustic phonetics. Language Monograph 23. Baltimore: Waverly Press.
Ladefoged, Peter. A course in phonetics. First edition, 1975. Second edition, 1982. Third edition, 1993. Fourth edition, 2001. Fifth edition, 2006. Sixth edition, 2011.
Ladefoged, Peter & Johnson, Keith. 2014. A course in phonetics. Seventh edition. Stamford, CT: Cengage Learning.
Lindsey, Geoff. 2013. The vowel space. http://englishspeechservices.com/blog/the-vowel-space/
Mattingly, Ignatius G. 1999. A short history of acoustic phonetics in the U.S. Proceedings of the XIVth International Congress of Phonetic Sciences. San Francisco, CA. 1-6.
Paget, Richard. 1930. Human speech. London: Routledge & Kegan Paul.
Potter, Ralph K. & Peterson, Gordon E. 1948. The representation of vowels and their movements. Journal of the Acoustical Society of America 20(4): 528-535.
Russell, George Oscar. 1928. The vowel, its physiological mechanism as shown by X-ray. Columbus: OSU Press.
I can see two ways in which this is true. First, a model of the human vocal tract consisting of two (or even more) formant values is far from accurate: the vocal tract can generate anti-formants, and even without that complication, the shape and material of the mouth and pharynx are not very much like those of a flute or clarinet; the vocal tract is a much more complex resonator. However, most of us are not interested in modeling this physical, biological object as such, nor, unless we are very much oriented towards articulatory phonetics, the movements of the tongue for their own sake. We are more interested in representing the aspects of vowel sounds that are important linguistically.
But here too, the conception that "vowels are things with two formants and a midpoint" is a substantial oversimplification. Most obviously, vowels extend over (more or less) time, and their properties can change (more or less) during this time. Both these aspects - duration and glide direction/extent - can be linguistically distinctive, although they often are not. So to fully convey the properties of a vowel, we will need to create a dynamic representation. While this creates challenges for measurement and especially for analysis, these problems are orthogonal to the question of how best to describe a vowel at a single point - more precisely, a short window - in time.
As mentioned, the "point" spectrum of a vowel sound, a function mapping frequency to amplitude, is complex. For one thing, it contains some information that is relatively speaker-specific. This data is of great importance in forensic and other speaker-recognition tasks, but in sociophonetic/LVC work we are usually happy to ignore it (if we even can). Other aspects of a vowel's spectrum, not necessarily easily separable from the first category, convey information about pitch, nasality, and the umbrella term "voice quality". These things may or may not interest us, depending on the language involved and the particular research being conducted.
And then there is "vowel quality" proper, which linguists generally describe using four pairs of terms: high-low (or closed-open), back-front, rounded-unrounded, and tense-lax. Originally, these parameters were thought of as straightforwardly articulatory, reflecting the position of the jaw, tongue, lips, and pharynx. As we will see, this articulatory view has shifted, but the IPA alphabet still uses the same basic terms (though no longer tense-lax), and for the most part Ladefoged & Johnson (2014) classify English vowels along the same dimensions as A. M. Bell (1867), who used primary-wide instead of tense-lax:
Equally long ago, scientists were beginning to realize that the vocal tract's first two resonances (or formants, as we now say) are related to the high-low and back-front dimensions of vowel quality, respectively. The higher the first formant (F1), the lower the vowel, and the higher the second formant (F2), the fronter the vowel. Helmholtz (1862/1877) partially demonstrated this with experiments holding a series of tuning forks up to the mouth, and he also made the first steps in vowel synthesis. But he found it difficult - like present-day researchers, sometimes - to distinguish F1 and F2 in back vowels, considering them simple resonances:
In contrast to Helmholtz, A. G. Bell (1879) and Hermann (1894) both emphasized that the resonance frequencies characterizing specific vowels were independent of the fundamental frequency (F0) of the voice. Bell provided an early description of formant bandwidth, while Hermann coined the term "formant" itself.
In the new century, experiments on the phonautograph, the phonograph, the Phonodeik, and other machines led most investigators to realize that all vowel sounds consisted of several formants (not just one for back vowels and two for front vowels, as Helmholtz had influentially claimed); advances were also made in vowel synthesis, using electrical devices. In particular, Paget (1930) argued for the importance of two formants for each vowel. But the most progress in acoustic phonetics was made after the invention of the sound spectrograph and its declassification following World War II.
Four significant publications from the immediate postwar years - Essner (1947), Delattre (1948), Joos (1948), and Potter & Peterson (1948) - all use spectrographic data to analyze vowels, and all four explicitly identify the high-low dimension with F1 (or "bar 1" for P & P) and the back-front dimension with F2 (or "bar 2" for P & P). Higher formants are variously recognized, but considered less important. In Delattre's analysis, the French front rounded vowels are seen to have lower F2 (and F3) values than the corresponding unrounded vowels:
Jakobson, Fant and Halle (1952) is somewhat different; it defines the acoustic correlates of distinctive phonological features, aiming to cover vowels and consonants with the same definitions. So the pair compact-diffuse refers to the relative prominence of a central spectral peak, while grave-acute reflects the skewness of the spectrum. In vowels, compact is associated with a more open tongue position and higher F1, and diffuse with a more closed tongue position and lower F1. Grave or back vowels have F2 closer to F1, acute or front vowels have F2 closer to F3. (Indeed, F2 - F1 has been suggested as an alternative to F2 for measuring the back-front dimension, e.g. in the first three editions of Ladefoged's Course on Phonetics).
These authors all more or less privilege an acoustic view of vowel differences over an articulatory view, noting that acoustic measurements may correspond better to the traditional "articulatory" vowel quadrilateral than the actual position of the tongue during articulation. The true relationship between articulation and acoustics was not well understood until Fant (1960). But the discrepancy had been suspected at least since Russell (1928), whose X-ray study showed that the highest point of the tongue was not directly related to vowel quality; it was noticeably higher in [i] than in [u], for example. In addition, certain vowel qualities, like [a], could be produced with several different configurations of the tongue. Observations like these led Russell to make the well-known claim that "phoneticians are thinking in terms of acoustic fact, and using physiological fantasy to express the idea".
Outside of a motor theory of speech perception, the idea that the vowel space is defined by acoustic resonances rather than articulatory configurations should be acceptable, although the integration of continuous acoustic parameters into phonological theory has never been smoothly accomplished. While we don't know that formant frequencies are directly tracked by our perceptual apparatus, it seems that they are far from fictional, at least from the point of view of how they function in language.
[To be continued in Part 2, with less history and more practical suggestions!]
References (the works by Harrington, Jacobi, and Lindsey, though not cited above, were useful in learning about the topic):
Bell, Alexander Graham. 1879. Vowel theories. American Journal of Otology 1: 163-180.
Bell, Alexander Melville. 1867. Visible Speech: The Science of Universal Alphabetics. London: Simkin, Marshall & Co.
Delattre, Pierre. 1948. Un triangle acoustique des voyelles orales du français. The French Review 21(6): 477-484.
Essner, C. 1947. Récherches sur la structure des voyelles orales. Archives Néerlandaises de Phonétique Expérimentale 20: 40-77.
Fant, Gunnar. 1960. Acoustic theory of speech production. The Hague: Mouton.
Harrington, Jonathan. 2010. Acoustic phonetics. In W. Hardcastle et al. (eds.), The Handbook of Phonetic Sciences, 2nd edition. Oxford: Blackwell.
Helmholtz, Hermann von. 1877. Die Lehre von den Tonempfindungen. 4th edition. Braunschweig: Friedrich Vieweg.
Hermann, Ludimar. 1894. Beiträge zur Lehre von der Klangwahrnehmung. Pflügers Archiv 56: 467-499.
Jacobi, I. 2009. On variation and change in diphthongs and long vowels of spoken Dutch. Ph.D. dissertation, University of Amsterdam.
Jakobson, Roman, Fant, C. Gunnar M., and Halle, Morris. 1952. Preliminaries to speech analysis: the distinctive features and their correlates. Cambridge: MIT Press.
Joos, Martin. 1948. Acoustic phonetics. Language Monograph 23. Baltimore: Waverly Press.
Ladefoged, Peter. A course in phonetics. First edition, 1975. Second edition, 1982. Third edition, 1993. Fourth edition, 2001. Fifth edition, 2006. Sixth edition, 2011.
Ladefoged, Peter & Johnson, Keith. 2014. A course in phonetics. Seventh edition. Stamford, CT: Cengage Learning.
Lindsey, Geoff. 2013. The vowel space. http://englishspeechservices.com/blog/the-vowel-space/
Mattingly, Ignatius G. 1999. A short history of acoustic phonetics in the U.S. Proceedings of the XIVth International Congress of Phonetic Sciences. San Francisco, CA. 1-6.
Paget, Richard. 1930. Human speech. London: Routledge & Kegan Paul.
Potter, Ralph K. & Peterson, Gordon E. 1948. The representation of vowels and their movements. Journal of the Acoustical Society of America 20(4): 528-535.
Russell, George Oscar. 1928. The vowel, its physiological mechanism as shown by X-ray. Columbus: OSU Press.
If Individuals Follow The Exponential Hypothesis, Groups Don't (And Vice Versa)
If you haven't heard of the Exponential Hypothesis, read this, this and this, and if you want more, look here. Guy's paper inspired me to want to do this kind of linguistics. But now it seems that the patterns he so cleverly explained were just meaningless coincidences - leaving this, uncontested, as the most impressive quantitative LVC paper of all time. But I digress.
Sociolinguists have differed for aeons regarding the relationship between the individual and the group. Even Labov's clear statements along the lines that "language is not a property of the individual, but of the community" are qualified, or undermined, by defining a speech community as "a group of people who share a given set of norms of language" (see also pp. 206-210 of the same paper for a staunch defense of the study of individuals).
The typical variationist recognizes the practical need to combine data from a group of speakers, even if their theoretical goal is the analysis of individual grammars. After some years spent in ignorance of the statistical ramifications of this situation, they have now generally adopted mixed-effects regression modeling as a way to have their cake and eat it too.
But the Exponential Hypothesis is not well-equipped to bridge this gap. If each individual i retains final t/d at a rate of ri for regular past tense forms, ri2 for weak past tense forms, and ri3 for monomorphemes - and if ri varies by individual (as has always been conceded) - then the pooled data from all speakers can never show an exponential relationship.
I will demonstrate this under four assumptions of how speakers might vary: 1) the probability of retention, r, is normally distributed across the population; 2) the probability of retention is uniformly (evenly) distributed over a similar range; 3) the log-odds of retention - log(r / (1 - r)) - is normally distributed; 4) the log-odds of retention is uniformly distributed.
Using a central value for r of +2 log-odds (.881), and allowing speakers to vary with a standard deviation of 1 (in log-odds) or 0.15 (in probability), I obtained the following results, with 100,000 speakers in each simulation:
| Probability Normal | Theoretical (Exponential) | Empirical (Group Mean) |
|---|---|---|
| Regular Past | .862 | .862 |
| Weak Past | .743 | .759 |
| Monomorpheme | .641 | .679 |
| Probability Uniform | Theoretical (Exponential) | Empirical (Group Mean) |
|---|---|---|
| Regular Past | .862 | .862 |
| Weak Past | .742 | .758 |
| Monomorpheme | .639 | .680 |
| Log-Odds Normal | Theoretical (Exponential) | Empirical (Group Mean) |
|---|---|---|
| Regular Past | .844 | .844 |
| Weak Past | .712 | .728 |
| Monomorpheme | .601 | .638 |
| Log-Odds Uniform | Theoretical (Exponential) | Empirical (Group Mean) |
|---|---|---|
| Regular Past | .842 | .842 |
| Weak Past | .710 | .724 |
| Monomorpheme | .598 | .633 |
These simulations assume an equal amount of data from each speaker, and an equal balance of words from each speaker (which matters if individual words vary). If these conditions are not met, like in real data, the groups will likely deviate even more from the exponential pattern. Looking at it the other way round, the very existence of an exponential pattern in pooled data - as is found for t/d-deletion in English! - is evidence that the true Exponential Hypothesis, for individual grammars, is false.
P.S. Why should this be, you ask? Let me try some math.
A function f(x) is strictly convex over an interval if the second derivative of the function is positive for all x in that interval.
Now let f(x) = xn, where n > 1. The second derivative is n · (n-1) · xn-2. Since n > 1, both n and (n-1) are positive. If x is positive, xn-2 is positive, making the second derivative positive, which means that xn is strictly convex over the whole interval 0 < x < ∞.
Jensen's inequality states that if x is a random variable and f(x) is a strictly convex function, then f(E[x]) < E[f(x)]. That is, if we take the expected value of a variable over an interval, and then apply a strictly convex function to it, the result is always less than if we apply the function first, and then take the expected value of the outcome.
In our case, x is the probability of t/d retention, and like all probabilities, it lies on the interval between 0 and 1, where we know xn is strictly convex. By Jensen's inequality, E[x]n < E[xn]. This means that if we take the mean rate of retention for a group of speakers, and raise it to some power, the result is always less than if we raise each speaker's rate to that power, and then take the mean.
Therefore, the theoretical exponential rate will always be less than the empirical group mean rate, which is what we observed in all the simulations above.
On Exactitude In Science: A Miniature Study On The Effects Of Typical And Current Context
In that Empire, the Art of Cartography attained such Perfection that the map of a single Province occupied the entirety of a City, and the map of the Empire, the entirety of a Province. In time, even these immense Maps no longer satisfied, and the Cartographers' Guilds surveyed a Map of the Empire whose Size was that of the Empire, and which coincided point for point with it. The following Generations, less addicted to the Study of Cartography, realized that that vast Map was useless, and not without some Pitilessness delivered it up to the Inclemencies of Sun and Winter. In the Deserts of the West, there remain tattered Ruins of that Map, inhabited by Animals and Beggars; in all the Land there is no other Relic of the Disciplines of Geography. (J. L. Borges)
A scientific model makes predictions based on a number of variables and parameters. The more complex the model, the more accurate its predictions. But all things being equal, a simpler model is preferred. As Newton put it: "We are to admit no more causes of natural things than such as are both true and sufficient to explain their appearances."
Exemplar Theory makes predictions about the present or future based on an enormous amount of stored information about the past. For example, a speaker is said to pronounce a word by taking into account the thousands of ways he or she has produced and heard it before. If such feats of memory are possible - I ain't sayin' I don't believe Goldinger 1998 - we should not be surprised by the accuracy of models that rely on them. And if language can be shown to rely on them, so be it. But the abandonment of parsimony, in the absence of clear evidence, should be resisted. (See the comment by S. Brown below for an alternative view of this issue.)
The same phenomena can often be accounted for "equally well" by a more deductive traditional theory or by a more inductive, bottom-up approach. The chemical elements were assigned to groups (alkali metals, halogens, etc.) because of their similar physical properties and bonding behavior long before the nuclear basis for these similarities was discovered. In biology, the various taxonomic branchings of species can be thought of as a reflection and continuation of their historical evolution, but the differences exist on a synchronic level as well - in organisms' DNA.
In classical mechanics, if an object begins at rest, its current velocity can be determined by integrating its acceleration over time. By storing the details of acceleration at every point along a trajectory, the current velocity can be calculated by integration: v(t) = ∫ a(t) dt. If we ride a bus with our eyes closed and our fingers in our ears, we can estimate our present speed if we remember everything about our past accelerations.
A free-falling object, under the constant acceleration of gravity, g, has velocity v(t) = g · t. But a block sliding down a ramp made up of various curved and angled sections, like a roller coaster, has an acceleration that changes with time. The acceleration at any moment is proportional to the sine of the slope of the ramp. Integrating, v(t) = g · ∫ sin(θ(t)) dt.
On a simple inclined plane, the angle is constant, so the acceleration is too. The velocity increases linearly: like free-fall, only slower. If the shape of the ramp is complicated, solving the integral of acceleration can be very difficult. (It might be beyond the capacity of the brain to calculate - but on a real roller coaster, we don't have to remember the past ten seconds to know how fast we are going now! We use other cues to accomplish that.)
But forgetting integration, we can solve for velocity in another way, showing that it depends only on the vertical height fallen: v = sqrt(2 · g · h). Obviously this is simpler than keeping track of complex and changing accelerations over time. This equation, rewritten as 1/2 · v2 = g · h, also reflects the balance between kinetic and potential energy, one part of the important physical law of conservation of energy. Instead of a near-truism with a messy implementation, we have an elegant and powerful principle.
Both expressions for velocity fit the same data, but to call the second an "emergent generalization", à la Bybee 2001, ignores its universality and demotivates the essential next step: the search for deeper explanations.
Admittedly, this physical allegory is unlikely to convince any exemplar theorists to recant. But we should realize that given its powerful and unexplanatory nature, any correct predictions made by ET do not constitute real evidence in its favor. We need to determine if the data also support an alternative theory, or at least find places where the data is more compatible with a weaker version of ET, rather than a stronger one.
A recently-discussed case suggests that with respect to phonological processes, individual words are not only influenced by their current contexts, but also, to a lesser degree, by their typical contexts (Guy, Hay & Walker 2008; Hay 2013). This is one of several recent studies by Hay and colleagues that show widespread and principled lexical variation, well beyond the idiosyncratic lexical exceptionalism sometimes acknowledged in the past, e.g. "when substantial lexical differences appear in variationist studies, they appear to be confined to a few lexical items" (Guy 2009).
The strong-ET interpretation is that all previous pronunciations of a word are stored in memory, and this gives us the typical-context distribution for each word. But if this is the case, the current-context effect must derive from something else: either from mechanical considerations or from analogy to other words. It can't also reflect sampling from sub-clouds of past exemplars, because that would cancel out the typical-context effect.
For words to be stored along with their environments is actually a weak version of word-specific phonetics (Pierrehumbert 2002). It is not that words are explicitly marked to behave differently; they only do so because of the environments they typically find themselves in. For Yang (2013: 6325), "these use asymmetries are unlikely to be linguistic but only mirror life." But whether they mirror life or reflect language-internal collocational structures, these asymmetries are not properties of individual words.
Under this model of word production - sampling from the population of stored tokens, then applying a constant multiplicative contextual effect - we observe the following pattern (in this case, the process is t/d-deletion, as in Hay 2013; the parameters are roughly based on real data):
Exemplar Model: Contextual Effect Greatest When Pool Is Least Reduced
This pattern has two main features: as words' typical contexts favor retention more, retention rates increase linearly before both V and C, with a widening gap between the two. From the Exemplar Theory perspective, when the pool of tokens contains mainly unreduced forms, the differences between constraints on reduction can be seen more clearly. But when many of the tokens in the pool are reduced already, the difference between pre-consonantal and pre-vocalic environments appears smaller. Such reduced constraint sizes are the natural result when a process of "pre-deletion" intersects with a set of rules or constraints that apply later, as discussed in this post, and in a slightly different sense in Guy 2007.
An alternative to storing every token is to say that words acquire biases from their contexts, and that these biases become properties of the words themselves. The source of a bias could be irrelevant to its representation - one word typically heard before consonants, another typically heard from African-American speakers, and another typically heard in fast speech contexts could all be marked for "extra deletion" in the same way.
From the point of view of parsimony, this is appealing. To figure out how a speaker might pronounce a word, the grammar would have to refer to a medium-sized list of by-word intercepts, but not search through a linguistic biography thick and complex enough to have been written by Robert Caro.
But the theoretical rubber needs to hit the empirical road, or else we are just spinning our wheels here. So, compared to the Stor-It-All model, does a stripped-down word-intercept approach make adequate predictions, or - dare we hope - even better ones? Are the predictions even that different?
If we assume that for binary variables, by-word intercepts (like by-speaker intercepts) combine with contextual effects additively on the log-odds scale (which seems more or less true), we obtain a pattern like this:
Intercept Model: Typical Context Combines W/ Constant Current Context
Although the two figures are not wildly different, we can see that in this case, there is no steady separation of the _V and _C effects as overall retention increases. The following-segment effect is constant in log-odds (by stipulation), and this manifests as a slight widening near the center of the distribution. The effects of current context and typical context are independent in this model, as opposed to what we saw above.
As usual, the Buckeye Corpus (Pitt et al. 2007) is a good proving ground for competing predictions of this kind. The Philadelphia Neighborhood Corpus has a similar amount of t/d coded (with more coming soon). Starting with Buckeye, I only included tokens of word-final t/d that were followed by a vowel or a consonant. I excluded all tokens with preceding /n/, in keeping with the sociolinguistic lore, "Beware the nasal flap!" I then restricted the analysis to words with at least 10 total tokens each - and excluded the word "just", because it had about eight times as many tokens as any of the other words. I was left with 2418 tokens of 69 word types.
Incidentally, there is no significant relationship between a word's overall deletion rate and its (log) frequency, whether the frequency measure is taken from the Buckeye Corpus itself (p = .15) or from the 51-million-word corpus of Brysbaert et al. 2013 (p = .37). The absence of a significant frequency effect on what is arguably a lenition process goes against a key tenet of Exemplar Theory (Bybee 2000, Pierrehumbert 2001), but the issue of frequency is not our main concern here.
I first plotted two linear regression lines, one for the pre-vocalic environments and one for the the pre-consonantal environments. The regressions were weighted according to the number of tokens for each word. I then tried a quadratic rather than a linear regression. However, these curves did not provide a significantly better fit to the data - p(_V) = .57, p(_C) = .46 - so I retreated to the linear models. The straight lines plotted below look parallel; in fact the slope of the _V line is 0.301 and the slope of the _C line is 0.369. Since the lines converge slightly rather than diverging markedly, this data is less consistent with the exemplar model sketched above, and more consistent with the word-intercept model.
Buckeye Corpus: Parallel Lines Support Intercept Model, Not Exemplars
One way to improve this analysis would be to use a larger corpus, at least for the x-axis, to more accurately estimate the proportion that a given word ending in t/d is followed by a vowel rather than a consonant. For example, the spoken section of COCA (Davies 2008-) is about 250 times larger than the Buckeye Corpus. Of course, for a few words the estimate from the local corpus might better represent those speakers' biases.
Turning finally to data from the Philadelphia Neighborhood Corpus, we see a fairly similar picture. Note that some of the words' left-right positions differ noticeably between the two studies. The word "most", despite having 150-200 tokens, occurs before a vowel 75% of the time in Philadelphia, but only 52% of the time in Ohio. It is hard to think what this could be besides sampling error, but if it is that, it casts some doubt on the reliability of these results, especially as most words have far fewer tokens.
Philadelphia Neighborhood Corpus: Convergence, Not Exemplar Prediction
Regarding the regression lines, there are two main differences. First, Philadelphia speakers delete much more before consonants than Ohio speakers, while there is no overall difference before vowels. This creates the greater following-segment effect noticed for Philadelphia before.
The second difference is that in Philadelphia, a word's typical context seems to barely affect its behavior before vowels. The slope before consonants, 0.317, is close to those observed in Ohio, but the slope before vowels is only 0.143 - not significantly different from zero (p = .14). Recall that under the exemplar model, the _V slope should always be larger than the _C slope; words almost always occurring before vowels - passed, walked, talked - should provide a pool of pristine, unreduced exemplars upon which the effects of current context should be most visible.
I have no explanation at present for the opposite trend being found in Philadelphia, but it is clear that neither the PNC data nor the Buckeye Corpus data show the quantitative patterns predicted by the exemplar theory model. This, and a general preference for parsimony - in storage, and arguably in computation (again, see S. Brown below) - points to typical-context effects being "ordinary" lexical effects. "[We] shall know a word by the company it keeps" (Firth 1957: 11), but we still have no reason to believe that the word itself knows all the company it has ever kept. And to find our way forward, we may not need a map at 1:1 scale.
Thanks: Stuart Brown, Kyle Gorman, Betsy Sneller, & Meredith Tamminga.
References:
Borges, Jorge Luis. 1946. Del rigor en la ciencia. Los Anales de Buenos Aires 1(3): 53.
Brysbaert, Marc, Boris New and Emmanuel Keuleers. 2013. SUBTLEX-US frequency list with PoS information final text version. Available online at http://expsy.ugent.be/subtlexus/.
Bybee, Joan. 2000. The phonology of the lexicon: evidence from lexical diffusion. In Michael Barlow and Suzanne Kemmer (eds.), Usage-based models of language. Stanford: CSLI. 65-85.
Bybee, Joan. 2001. Phonology and language use. Cambridge Studies in Linguistics 94. Cambridge: Cambridge University Press.
Davies, Mark. 2008-. The Corpus of Contemporary American English: 450 million words, 1990-present. Available online at http://corpus.byu.edu/coca/.
Firth, John R. 1957. A synopsis of linguistic theory, 1930-1955. In Studies in Linguistic Analysis, Special volume of the Philological Society. nOxford: Basil Blackwell.
Guy, Gregory. 2007. Lexical exceptions in variable phonology. Penn Working Papers in Linguistics 13(2), Papers from NWAV 35, Columbus.
Guy, Gregory. 2009. GoldVarb: Still the right tool. NWAV 38, Ottawa.
Guy, Gregory, Jennifer Hay and Abby Walker. 2008. Phonological, lexical, and frequency factors in coronal stop deletion in early New Zealand English. LabPhon 11, Wellington.
Hay, Jennifer. 2013. Producing and perceiving "living words". UKLVC 9, Sheffield.
Pierrehumbert, Janet. 2001. Exemplar dynamics: word frequency, lenition and contrast. In Joan Bybee and Paul Hopper (eds.), Frequency and the emergence of linguistic structure. Amsterdam: John Benjamins. 137-157.
Pierrehumbert, Janet. 2002. Word-specific phonetics. Laboratory Phonology 7. Berlin: Mouton de Gruyter. 101-139.
Pitt, Mark A. et al. 2007. Buckeye Corpus of Conversational Speech. Columbus: Department of Psychology, Ohio State University.
Yang, Charles. 2013. Ontogeny and phylogeny of language. Proceedings of the National Academy of Sciences 110(16): 6324-6327.
Random Slopes: Now That Rbrul Has Them, You May Want Them Too
I've made the first major update to Rbrul in a long time, adding support for random slopes. While in most cases, models with random intercepts perform better than those without them, a recent paper (Barr et al. 2013) has convincingly argued that for each fixed effect in a mixed model, one or more corresponding random slopes should also be considered.
So what are random slopes and what benefits do they provide? If we start with the simple regression equation y = ax + b, the intercept is b and the slope is a. A random intercept allows b to vary; if the data is drawn from different speakers, each speaker essentially has their own value for b. A random slope allows each speaker to have their own value for a as well.
The sociolinguistic literature usually concedes that speakers can vary in their intercepts (average values or rates of application). But at least since Guy (1980), it has been suggested or assumed that the speakers in a community do not vary in their slopes (constraints). As we saw last week, though, in some data sets the effect of following consonant vs. vowel on t/d-deletion varies by speaker more than might be expected by chance.
In the Buckeye Corpus, the estimated standard deviation, across speakers, of this consonant-vs.-vowel slope was 0.70 log-odds; in the Philadelphia Neighborhood Corpus, it was 0.67. A simulation reproducing the number of speakers, number of tokens, balance of following segments, overall following-segment effect, and speaker intercepts produced a median standard deviation of only 0.10 for Ohio and 0.16 for Philadelphia. Speaker slopes as dispersed as the ones actually observed would occur very rarely by chance (Ohio, p < .001; Philadelphia, p = .003).1
If rates and constraints can vary by speaker, it is important not to ignore speaker when analyzing the data. In assessing between-speaker effects – gender, class, age, etc. – ignoring speaker is equivalent to assuming that every token comes from a different speaker. This greatly overestimates the significance of these between-speaker effects (Johnson 2009). The same applies to intercepts (different rates between groups) and slopes (different constraints between groups). The figure below illustrates this.
By keeping track of speaker variation, random intercepts and slopes help provide accurate p-values (left). Without them, data gets "lumped" and p-values can be meaninglessly low (right).
Especially if your data is unbalanced, there are other benefits to using random slopes if your constraints might differ by speaker (or by word, or another grouping factor); these will not be discussed here. Mixed-effects models with random slopes not only control for by-speaker constraint variation, they also provide an estimate of its size. Mixed models with only random intercepts, like fixed-effects models, rather blindly assume the slope variation to be zero, and are only accurate if it really is. No doubt, this "Shared Constraints Hypothesis" (Guy 2004) is roughly, qualitatively correct: for example, all 83 speakers from Ohio and Philadelphia showed more deletion before consonants than before vowels (except one person with only two tokens!) But the hypothesis has been taken for granted far more often than it has been supported with quantitative evidence.
Rbrul has always fit models with random intercepts, allowing users to stop assuming that individual speakers have equal rates of application of a binary variable (or the same average values of a continuous variable). Now Rbrul allows random slopes, so the Shared Constraints Hypothesis can be treated like the hypothesis it is, rather than an inflexible axiom built into our software. The new feature may not be working perfectly, so please send feedback to danielezrajohnson@gmail.com (or comment here) if you encounter any problems or have questions. Also feel free to be in touch if you have requests for other features to be added in the future!
1These models did not control for other within-subjects effects that could have increased the apparent diversity in the following-segment effect.
P.S. A major drawback to using random slopes is that models containing them can take a long time to fit, and sometimes they don't fit at all, causing "false convergences" and "singular convergences" that Rbrul reports with an "Error Message". There is not always a solution to this – see here and here for suggestions from Jaeger – but it is always a good idea to center any continuous variables, or at least keep the zero-point close to the center. For example, if you have a date-of-birth predictor, make 0 the year 1900 or 1950, not the year 0. Add random slopes one at a time so processing times don't get out of hand too quickly. Sonderegger has suggested dropping the correlation terms that lmer() estimates (by default) among the random effects. While this speeds up model fitting considerably, it seems to make the questionable assumption that the random effects are uncorrelated, so it has not been implemented.
P.P.S. Like lmer(), Rbrul will not stop you from adding a nonsensical random slope that does not vary within levels of the grouping factor. For example, a by-speaker slope for gender makes no sense because a given speaker is – at least traditionally – always the same gender. If speaker is the grouping factor, use random slopes that can vary within a speaker's data: style, topic, and most internal linguistic variables. If you are using word as a grouping factor, it is possible that different words show different gender effects; using a by-word slope for gender could be revealing.
P.P.P.S. I also added the AIC (Akaike Information Criterion) to the model output. The AIC is the deviance plus two times the number of parameters. Comparing the AIC values of two models is an alternative to performing a likelihood-ratio test. The model with lower AIC is supposed to be better.
References:
Barr, Dale J., Roger Levy, Christoph Scheepers, and Harry J. Tily. 2013. Random effects structure for confirmatory hypothesis testing: keep it maximal. Journal of Memory and Language 68: 255-278. [pdf]
Guy, Gregory R. 1980. Variation in the group and the individual: the case of final stop deletion. In W. Labov (ed.), Locating language in time and space. New York: Academic Press. 1-36. [pdf]
Guy, Gregory R. 2004. Dialect unity, dialect contrast: the role of variable constraints. Talk presented at the Meertens Institute, August 2004.
Johnson, Daniel E. 2009. Getting off the GoldVarb standard: introducing Rbrul for mixed-effects variable rule analysis. Language and Linguistics Compass 3(1): 359-383. [pdf]
Testing The Logistic Model Of Constant Constraint Effects: A Miniature Study
Sociolinguistics, like other fields, decided during the 1970s that logistic regression was the best way to analyze the effects of contextual factors on binary variables. Labov (1969) initially conceived of the probability of variable rule application as additive: p = p0 + pi + pj + … . Cedergren & Sankoff (1974) introduced the multiplicative model: p = p0 × pi × pj × … . But it was a slightly more complex equation that eventually prevailed: log(p/(1-p)) = log(p0/(1-p0)) + log(pi/(1-pi)) + log(pj/(1-pj)) + … .
Sankoff & Labov (1979: 195-6) note that this "logistic-linear" model "replaced the others in general use after 1974", although it was not publicly described until Rousseau & Sankoff (1978). It has specific advantages for sociolinguistics (treating favoring and disfavoring effects equally), but it is identical to the general form of logistic regression covered in e.g. Cox (1970). The VARBRUL and GoldVarb programs (Sankoff et al. 2012) apply Iterative Proportional Fitting to log-linear models (disallowing "knockouts" and continuous predictors). Such models are equivalent to logistic models, with identical outputs (pace Roy 2013).
The logistic transformation, devised by Verhulst in 1838, was first used to model population growth over time (Cramer 2002). If a population is limited by a maximum value (which we label 1.0), and the rate of increase is proportional to both the current level p and the remaining room for expansion 1-p, then the population, over time, will follow an S-shaped logistic curve, with a location parameter a and a slope parameter b:
p = exp(a+bt)/(1+exp(a+bt)). We see several logistic curves below.
Its origin in population growth curves makes logistic regression a natural choice for analyzing discrete linguistic change, and it is extensively used in historical syntax (Kroch 1989) and increasingly in phonology (Fruehwald et al. 2009). However, if the independent variable is anything other than time, it is fair to ask whether its effect actually has the signature S-shape.
For social factors, which rarely resemble continuous variables, this is difficult to do. Labov's charts - juxtaposed in Silverstein (2003) - show that in mid-1960's New York, the effect of social class on the (r) variable and the (th) variable were quite different. For (r), the social classes toward the edges of the hierarchy are more dispersed; the lower classes (0 vs. 1) are further apart than the working classes (2-3 vs. 4-5). This is the opposite of a logistic curve, which always changes fastest in the middle. However, (th) shows a different pattern, which is more consistent with a S-curve: the lower and working classes are similar, with a large gap between them and the middle class groups. Finally, while it is hard to judge, neither variable appears to respond to contextual style in a clearly sigmoid manner.
Linguistic factors offer a better approach to the question. Rather than observe the shape of the response to a multi-level predictor - the levels of linguistic factors are often unordered - we can compare the size of binary linguistic constraints among speakers who vary in their overall rates of use. The idea that speakers in a community (and sometimes across community lines) use variables at different rates while sharing constraints began as a surprising observation (Labov 1966, G. Sankoff 1973, Guy 1980) but has become an assumption of the VARBRUL/GoldVarb paradigm (Guy 1991, Lim & Guy 2005, Meyerhoff & Walker 2007, Tagliamonte 2011; but see also Kay 1978, Kay & McDaniel 1979, Sankoff & Labov 1979).
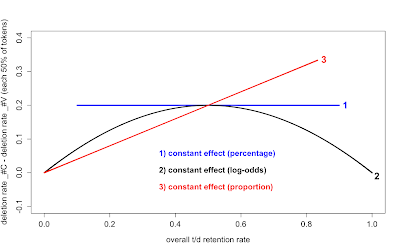
Recently, speaker variation has motivated the introduction of mixed-effects models with random speaker intercepts. But if the variable in question is binary (and the regression is therefore logistic), a constant effect (in logistic terms) should have larger consequences (in percentage terms) in the middle of the range. If speaker A, in a certain context, shifts from 40% to 60% use, then speaker B should shift from 80% to 90% - not 100%. These two changes are equal in logistic units (called log-odds): log(.6/(1−.6)) − log(.4/(1−.4)) = log(.9/(1−.9)) − log(.8/(1−.8)) = 0.811.
In a classic paper, Guy (1980) compared the linguistic constraints on t/d-deletion for many individuals, but (despite the late year) presented factor weights from the multiplicative model, making it impossible to evaluate the relationship between rates and constraints from his tables. Therefore, we will use the following t/d data sets to attempt to address the issue:
Daleszynska (p.c.): 1,998 tokens from 30 Bequia speakers.
Labov et al. (2013): 14,992 tokens from 42 Philadelphia speakers.
Pitt et al. (2007): 13,664 tokens from 40 Central Ohio speakers.
Walker (p.c.): 4,022 tokens from 48 Toronto speakers.
The t/d-deletion predictor to be investigated is following consonant (west coast) vs. following vowel (west end). In most varieties of English, a following consonant favors deletion, while a following vowel disfavors it. Because the consonant-vowel difference has an articulatory basis, we might expect it to remain fairly constant across speakers. But if so, will it be constant in percentage terms, or in logistic terms? In fact, if deletion before consonants is a "late" phonetic process (caused by overlapping gestures?), we might observe a third pattern, where the effect would be smaller in proportion to the amount of deletion generated "earlier".1
That is, if a linguistic factor - e.g. following consonant vs. vowel in the case of t/d-deletion - has a constant effect in percentage terms, we find a horizontal line (1). If the constraint is constant in log-odds terms, as assumed by logistic regression, we see a curve with a maximum at 50% overall retention (2). If the effect arises from "extra" deletion before consonants, it increases in proportion to the overall retention rate (3).
Comparing the four community studies leads to some interesting results. There is a lot of variation between speakers in each community. We already knew that speakers varied in their overall rates of deletion, but the ranges here are wide. In Philadelphia, the median deletion level is 51%, but the range extends from 22% to 71% (considering people with more than 50 tokens). In the Ohio (Buckeye) corpus, the median rate was lower, 41%, with an even larger range, 18% to 73%. The Torontonians (with less deletion) and the Bequians (with more) also varied widely.
We also observe that speakers within communities differ in the observed following-segment effect. For example, in Philadelphia there were two speakers with very similar overall deletion rates, but one deleted 94% of the time before consonants and only 6% before vowels, while the other had 76% deletion before consonants and 20% before vowels. In Ohio, the consonant-vowel effect was smaller overall, with at least as much between-speaker variation: one speaker produced 79% deletion _#C and 4% _#V, while another produced 51% deletion _#C and 38% _#V. While it would require a statistical demonstration, this amount of divergence is probably more than would be expected by chance. If this is the case, even within speech communities, then we may need to take more care to model speaker constraint differences (for example, with random slopes).
Excludes speakers with <10 tokens, preceding /n/ and following /t, d/.
What about differences between communities? Clearly, the average deletion rates of the four communities differ: Bequia, the Caribbean island, has the most t/d deletion, while Canada's largest city shows the least. The white American communities are intermediate. Such differences are to be expected. What is more interesting is that the largest absolute following-segment effect is found in Philadelphia, where the data is closest to 50% average deletion. Ohio and Toronto, with around 40% deletion, show a smaller effect, in percentage terms. Bequia, with average deletion of nearly 90%, shows no clear following-segment effect at all. These findings are consistent with the logistic interpretation. The effect may be constant - but on the log-odds scale. On the percentage scale, it appears greatest in Philadelphia, where the median speaker shows a difference of 91% _#C vs. 16% _#V. But an effect this large - almost 4 log-odds - should show up in Bequia, yet it does not (of course, the Bequia variety is quite distinct from the others treated here; could it lack this basic constraint?).
Within each community, the logistic model predicts the same thing: the closer a speaker is to 50% deletion overall, the larger the consonant-vowel difference should appear. The data suggest that this prediction is borne out, at least to a first approximation. In Philadelphia, Ohio, and Toronto, all the largest effects are found in the 40% - 60% range, and the smallest effects mostly occur outside that range. While the following-segment constraint differs across communities (larger in Philadelphia, smaller in Bequia), and probably across individual speakers, it seems to follow an inherent arch-shaped curve, similar to (2). A cubic approximation of this curve is superimposed below on the data from all four communities.
In conclusion, the evidence from four studies of t/d-deletion suggests that speaker effects and phonological effects combine additively on a logistic scale, supporting the standard variationist model. However, both rates and constraints can vary, not only between communities, but within them.
Thanks to Agata Daleszynska, Meredith Tamminga, and James Walker.
1A diagonal also results from the "lexical exception" theory (Guy 2007), where t/d-deletion is bled when reduced forms are lexicalized, creating an' alongside and. When a word's underlying form may already be reduced, any contextual effects - like that of following segment - will be smaller in proportion. But if individual-word variation is part of the deletion process, we would expect the logistic curve (2) rather than the diagonal line (3).
References:
Cedergren, Henrietta and David Sankoff. 1974. Variable rules: Performance as a statistical reflection of competence. Language 50(2): 333-355.
Cox, David R. 1970. The analysis of binary data. London: Methuen.
Cramer, Jan S. 2002. The origins of logistic regression. Tinbergen Institute Discussion Paper 119/4. http://papers.tinbergen.nl/02119.pdf.
Fruehwald, Josef, Jonathan Gress-Wright, and Joel Wallenberg. 2009. Phonological rule change: the constant rate effect. Paper presented at North-Eastern Linguistic Society (NELS) 40, MIT. ling.upenn.edu/~joelcw/papers/FGW_CRE_NELS40.pdf.
Guy, Gregory R. 1980. Variation in the group and the individual: the case of final stop deletion. In W. Labov (ed.), Locating language in time and space. New York: Academic Press. 1-36.
Guy, Gregory R. 1991a. Explanation in variable phonology: an exponential model of morphological constraints. Language Variation and Change 3(1): 1-22.
Guy, Gregory R. 1991b. Contextual conditioning in variable lexical phonology. Language Variation and Change 3(2): 223-240.
Guy, Gregory R. 2007. Lexical exceptions in variable phonology. Penn Working Papers in Linguistics 13(2), Papers from NWAV 35. repository.upenn.edu/pwpl/vol13/iss2/9
Kay, Paul. 1978. Variable rules, community grammar and linguistic change. In D. Sankoff (ed.), Linguistic variation: models and methods. New York: Academic Press. 71-83.
Kay, Paul and Chad K. McDaniel. 1979. On the logic of variable rules. Language in Society 8(2): 151-187.
Labov, William. 1966. The social stratification of English in New York City. Washington, D.C.: Center for Applied Linguistics.
Labov, William. 1969. Contraction, deletion, and inherent variability of the English copula. Language 45(4): 715-762.
Labov, William et al. 2013. The Philadelphia Neighborhood Corpus of LING560 Studies. fave.ling.upenn.edu/pnc.html.
Lim, Laureen T. and Gregory R. Guy. 2005. The limits of linguistic community: speech styles and variable constraint effects. Penn Working Papers in Linguistics 13.2, Papers from NWAVE 32. 157-170.
Meyerhoff, Miriam and James A. Walker. 2007. The persistence of variation in individual grammars: copula absence in ‘urban sojourners’ and their stay‐at‐home peers, Bequia (St. Vincent and the Grenadines). Journal of Sociolinguistics 11(3): 346-366.
Pitt, M. A. et al. 2007. Buckeye Corpus of Conversational Speech. Columbus, OH: Department of Psychology, Ohio State University. buckeyecorpus.osu.edu.
Rousseau, Pascale and David Sankoff. Advances in variable rule methodology. In D. Sankoff (ed.), Linguistic Variation: Models and Methods. New York: Academic Press. 57-69.
Roy, Joseph. 2013. Sociolinguistic Statistics: the intersection between statistical models, empirical data and sociolinguistic theory. Proceedings of Methods in Dialectology XIV in London, Ontario.
Sankoff, David, Sali Tagliamonte, and Eric Smith. 2012. Goldvarb LION: A variable rule application for Macintosh. Department of Linguistics, University of Toronto.
Sankoff, David and William Labov. 1979. On the uses of variable rules. Language in Society 8(2): 189-222.
Sankoff, Gillian. 1973. Above and beyond phonology in variable rules. In C.-J. N. Bailey & R. W. Shuy (eds), New ways of analyzing variation in English. Washington, D.C.: Georgetown University Press. 44-61.
Silverstein, Michael. 2003. Indexical order and the dialectics of sociolinguistic life. Language & Communication 23(3-4): 193-229.
Tagliamonte, Sali A. 2011. Variationist sociolinguistics: change, observation, interpretation. Hoboken, N.J.: Wiley.
Subscribe to:
Posts (Atom)